Theory

Goal

Our project is to build an ab initio simulation tool able to calculate all the X-ray spectroscopies related to the electronic transition between core and valence states, occupied or not. It is more specifically applied to the X-ray absorption (XAS)  and emission (XES) close to the edge (XANES and VtoC XES). This concerns also the associated techniques depending on the polarization: linear dichroism, magnetic (XMCD) or natural circular dichroism. It is also applied to the resonant process, absorption-emission, the resonant x-ray diffraction  (with the different acronyms RXD, RXS, DAFS or DANES) as well as to the non-resonant inelastic x-ray scattering (NRIXS or X-Raman), and for the simulation of the electron energy loss spectroscopy (EELS) carried out in the transmission electron microscopes. Recently, we have also developed the simulation of surface resonant x-ray diffraction (SRXRD). Resonant Inelastic X-ray Scattering (RIXS) is actually under construction.

Calculation Methods

The calculation of the absorption or emission cross sections, or of the resonant form factors, needs first a good evaluation of the electronic structure around the absorbing atoms. For this purpose, FDMNES uses the density functional theory (DFT) with a local exchange-correlation potential eventually spin-dependent (LSDA). The Hubbard correction (LSDA + U) can also be utilized. The code is fully relativistic and thus takes into account the spin-orbit in core and optionally also in the valence and photoelectron states.

Two techniques can be selected by the user: the finite difference method (FDM)⁽¹⁾ which gives the name to the code, and the multiple scattering theory (MST). This last uses the “muffin-tin” approximation on the shape of the potential and is less precise but faster than the former.
The program can make a self-consistent calculation of the electronic structure before the final spectrum evaluation.⁽²⁾

FDMNES works in direct space. The electronic structure is calculated inside clusters of chosen radius around each of the absorbing atoms.
When the material is periodical, FDMNES makes automatically the symmetry analysis of the (magnetic) space group and takes in charge the building of the different clusters. The punctual groups of the clusters are also analyzed to benefit from their symmetry properties in term of computation efficiency. At the end, the code gives the total signal coming from all the atoms of the unit cell or of the molecule.

Another theoretical frame beyond DFT has been developped. It is the  time dependent DFT (TDDFT)⁽³⁾, which takes into account a part of the interaction between the core-hole and the photoelectron states. It is useful when these states are localized what is most often the case at the L₂₃ edges of the transition metals. In its actual state, the kernel, principal node of this theory is nevertheless local. One thus cannot get the so-called “excitonic” structures.

Outputs

Absorption cross section and dichroism

The absorption cross section is given for the unit cell or the molecule in Megabarn. Optionally the response function of the single sites can also be extracted. Linear and circular dichroism, magnetic or not, can also be calculated depending on the polarization and wave-function conditions of the x-ray beam illuminating the sample.

Resonant diffraction

Resonant diffraction is an elastic photon in – photon out process occuring also around the absorption edges and, related 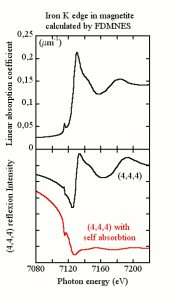to the electronic transition between core and non-occupied states. The formalism to calculate the resonant form factors is thus clothely related to the one used to get the absorption cross sections. FDMNES calculates them in a unified frame. The calculation of the final intensity for all the wanted diffraction peaks needs also the evaluation of the non resonant electric and magnetic form factors.
The code also takes into account the self-absorption correction and the birefringence effect. The intensity of the reflections is calculated for any conditions of incoming or outgoing polarizations.

From 2017, resonant scattering is also considered for surface diffraction (SRXRD). Crystal truncation rods (CTR) at any energy and spectra at any point of the CTR can be calculated. Simulations can be done for any kind of surfaces with adsorbates or ultra-thin films.⁽⁴⁾

X-ray Raman and EELS

In X-ray Raman and EELS, the response function of the spectroscopy is related to the energy loss of the incoming beam, close to an edge energy and to the momuntum transfert q. In practice the formula giving the resulting inelastic scattering amplitude is very close to the one for the absorption cross section. The absorption/emission transition operator is simply substituted by an exp(iq.r). This exponential is then expanded in spherical harmonics and Bessel functions.⁽⁵⁾  One finally gets the inelastic scattering intensity with its dependence versus q and the appearance of the so-called monopole contribution.

Density of states and COOP

To get a better understanding of the material and in addition to the x-ray spectra, the code can give the partial density of states projected (pDOS) on the atoms. It also gives the Crystal Overlap Occupation Population (COOP) which are a measurement of the covalency bounds between 2 atoms.⁽⁶⁾ COOP and pDOS can also be directly related to most of the features in the x-ray spectra.

Multipole expansion

For the physical analysis of the terms involved in the absorption or in the scattering of the photons, tensorial developments, in spherical or Cartesian basis, are realized.
They are applied for all the electric transition channels, dipole (E1), quadrupole (E2) or octupole (E3), or magnetic dipole (M1) and thus to all the crossing terms (E1E1, E1E2, E2E2, E1E3, M1M1, E1M1,…)

Comparison with experiment

It is possible to compare calculated spectra with experimental spectra in XANES and in resonant diffraction using confidence factors. One can also fit parameters such as the atomic positions, the atomic charges or the ones governing the convolution.

Numerical aspect

In 2015, thanks to the work of Sergey Guda, Alexander Guda, Mikhail Soldatov et al., Rostov, Russia⁽⁷⁾, the code in its finite difference mode became highly faster, up to 40 times. This was made possible by the use of the MUMPS library⁽⁸⁾, which efficiently solves systems of linear equation with sparse matrices. This makes possible the calculation also for systems with no symmetry and for large cluster radius.

User friendly

A very important part of our work aims to provide a user friendly code. Input data files are thought to be as simple as possible. For most calculations, users need only to furnish the atomic structure, possibly through cif or pdb files, the energy range to calculate, the edge and the atomic number of the absorbing atom. In the case of more specific calculations as dichroism, XES, X-ray Raman, RXD,… some more information is needed. It can be found in the provided manual and in the set of input data file examples.

---

⁽¹⁾ Y. Joly
X-ray absorption near edge structure calculations beyond the muffin-tin approximation
Phys. Rev. B 63, 125120-125129 (2001).
DOI: 10.1103/PhysRevB.63.125120

⁽²⁾ O. Bunau and Y. Joly
Self-consistent aspects of x-ray absorption calculations
J. Phys.: Condens. Matter 21, 345501 (2009).
DOI: 10.1088/0953-8984/21/34/345501

⁽³⁾ Oana Bunau and Yves Joly
Time-dependent density functional theory applied to x-ray absorption spectroscopy
Phys. Rev. B 85, 155121 (2012).
DOI: 10.1103/PhysRevB.85.155121

⁽⁴⁾ Yves Joly, Chiara Cavallari, Sergey A. Guda, and Christoph Sahle
Full potential simulation of x-ray Raman scattering spectroscopy
J. Chem. Theory Comput. 13, 2172-2177 (2017).
DOI: 10.1021/acs.jctc.7b00203

⁽⁵⁾ Maria Diaz-Lopez, Sergey A. Guda and Yves Joly
Crystal Orbital Overlap Population and X‑ray Absorption Spectroscopy
Phys. Chem. A 124, 6111–6118 (2020).
DOI: 10.1021/acs.jpca.0c04084

⁽⁶⁾ Yves Joly, Antoine Abisset, Aude Bailly, Maurizio De Santis, Farid Fettar,
Stéphane Grenier, Danny Mannix, Aline Y. Ramos, Marie-Claire Saint-Lager, Yvonne Soldo-Olivier, Jean-Marc Tonnerre, Sergey A. Guda, and Yvonne Gründer
Simulation of surface resonant x-ray diffraction
J. Chem. Theory Comput. 14, 973-980 (2018).
DOI: 10.1021/acs.jctc.7b01032

⁽⁷⁾ Sergey A. Guda, Alexander A. Guda, Mikhail A. Soldatov, Kirill A. Lomachenko, Aram L. Bugaev, Carlo Lamberti, Wojciech Gawelda, Christian Bressler, Grigory Smolentsev, Alexander V. Soldatov, Yves Joly
Optimized Finite Difference Method for the Full-Potential XANES Simulations: Application to Molecular Adsorption Geometries in MOFs and Metal-Ligand Intersystem Crossing Transients
J. Chem. Theory Comput. 11, 4512-4521 (2015).
DOI: 10.1021/acs.jctc.5b00327

⁽⁸⁾ P. R. Amestoy, I. S. Duff, J. Koster and J.-Y. L’Excellent,
A fully asynchronous multifrontal solver using distributed dynamic scheduling,
SIAM Journal on Matrix Analysis and Applications, Vol 23, No 1, pp 15-41 (2001).
DOI: 10.1137/S0895479899358194